

"Ich glaube es ging um Graphentheorie. Komm, lass uns den Raum suchen,
ich erzähl dir inzwischen, was es mit diesem Schwachsinnsbeweis auf sich
hat."
Während sie einen von den riesigen Wegweisern suchten, die sonst an jeder
Ecke standen, sich aber jetzt hartnäckig versteckten, erzählte Emmy:
"1852 färbte ein Engländer eine britische Landkarte. Gebiete,
die eine gemeinsame Grenze hatten, bekamen verschiedene Farben. Erstaunlicherweise
reichten ihm dafür vier Farben.
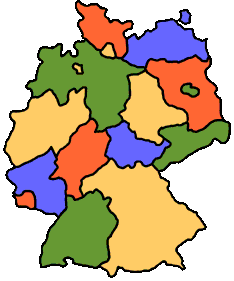
Die Bundesländer in vier Farben
Er fragte seinen Bruder, der Mathe studierte, ob das bei jeder Landkarte so
sei."
Max unterbrach Emmy.
"Das kann ich mir nicht vorstellen. In diesem verworrenen Haus hier braucht
man bestimmt zehn Farben um die Räume so zu färben."
"Nein, 1977 wurde endlich bewiesen, dass vier Farben immer reichen. Dazu
wurden alle denkbaren - und das sind unendlich viele - Karten in 1482 mögliche
Fälle zusammengefasst. Dann wurden sie mit einem Computer durchgetestet.
Und das spaltet die mathematische Welt. Viele denken, dass das kein Beweis ist,
weil er nicht von einem Menschen nachvollzogen werden kann."
"Darüber haben die sich also vorhin so gefetzt. Emmy, wir finden
den Graphentheorieraum einfach nicht."
"Willst du trotzdem was über Telefonnetze, Routenplaner oder Heiratsprobleme
hören?"
"Das hat alles was mit Graphen zu tun? Was ist denn eigentlich ein Graph?"
"Du kennst doch sicher das Haus vom Nikolaus?"
Max nickte, zog ein Blatt Papier und einen Bleistift aus seinem Rucksack und
zeichnete ein Nikolaushaus.
"Das ist ein Graph, ein paar Punkte, von denen manche miteinander verbunden
sind?"
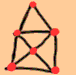
"Ja. Das Haus vom Nikolaus kann in einem Strich gezeichnet werden. Das
funktioniert aber nicht bei jedem Graphen, schau hier", und Emmy zeichnete
einen Graphen.

"In diesem Graphen gibt es vier Ecken mit drei Kanten.
Wenn du durch so eine Ecke zeichnest, lässt du immer eine Kante übrig,
und wenn du zurück kommst, bleibst du stecken."
"Aber das Haus vom Nikolaus hat doch auch zwei Ecken mit drei Kanten."
"Das funktioniert trotzdem: du kannst in einer starten, und in der anderen
aufhören."
"Oh, deshalb muss ich in einer der beiden unteren Ecken anfangen und auch
wieder aufhören. Und was hat das mit Heiratsproblemen zu tun?"
"Fangen wir erstmal mit den Telefonnetzen an. Jedes Telefon wird durch
eine Ecke gekennzeichnet, jedes Kabel durch eine Kante.
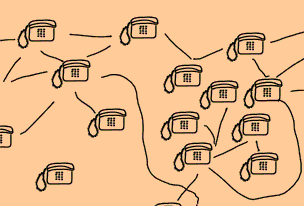
Eine interessante Frage ist, wie das Telefonnetz am besten gebaut werden kann,
damit alle Gespräche durchkommen und die Kosten möglichst gering sind.
Ein ganz ähnliches Problem steht beim Routenplaner."
"Macht das nicht der Computer?"
"Naja, die Graphentheorie entwickelt die Methoden, die die Computer dann
verwenden. Die meisten von den Fragen sind übrigens auch für Computer
sehr schwer. Für sehr große Graphen dauert das ewig."
"Und das Heiraten?"
"Der Heiratssatz von Hall sagt, dass in einer rein heterosexuellen Gesellschaft
mit genauso vielen Frauen wie Männern alle verheiratet werden können.
Zumindest wenn es für jede beliebige Gruppe von Frauen mindestens genauso
viele Männer gibt, die sich für wenigstens eine der Frauen interessieren.
Andersrum stimmt das übrigens auch."
"Der Herr Hall hatte ja ziemlich altertümliche Vorstellungen. Guck
mal da, direkt um die Ecke hätten wir einen Wegweiser gefunden."
"Na dann mal los, suchen wir uns einfach den nächsten Raum."
Anmerkung der Redaktion: Hier ein paar Graphentheorie-Links:
Die Graphentheorie hat ihren Ursprung im
Königsberger Brückenproblem
Über kürzeste Wege in Graphen
Über das Vierfarbenproblem